1. 10个常用的麦克劳林公式
$f(x)$在$ x0$处的n阶泰勒公式 $$ f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2} f''(x_0)(x-x_0)^2+…+\frac{1}{n!} f^{(n)} (x_0)(x-x_0)^n+R_n $$
$$ \sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}+(-1)^{n-1}\frac{x^{2n-1}}{(2n-1)!} +o(x^{2n}) $$ $$\arcsin x=x+\frac{x^3}{6}+o(x^3) $$ $$\tan x=x+\frac{x^3}{3}+o(x^3) $$ $$\arctan x=x-\frac{x^3}{3}+o(x^3) $$ $$\ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}+(-1)^{n-1}\frac{x^{n}}{n}+o(x^n) $$ $$e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3!} +\frac{x^n}{n!}+o(x^n) $$ $$(1+x)^\alpha=1+\alpha x+\frac{\alpha(\alpha-1)x^2}{2}+\frac{\alpha(\alpha-1)…(\alpha-n+1)}{n!} x^n+o(x^n)$$ $$\cos x=1-\frac{x^2}{2}+\frac{x^4}{4!}+(-1)^{n}\frac{x^{2n}}{(2n)!} +o(x^{2n}) $$
$$\frac{1}{1+x}=1-t+t^2-t^3+…+(-1)^nt^n$$ $$\frac{1}{1-x}=1+t+t^2+t^3+…+t^n$$
重要极限
$$ \lim_{x \to 0}\frac{e-(1+x)^{\frac{1}{x}}}{x}=\lim_{x \to \infty} x[e-(1+\frac{1}{x})^x]=\frac{e}{2} $$
2. 等价无穷小
$$x \to 0时$$ $$\sin x\sim x$$ $$\arcsin x\sim x$$ $$\tan x\sim x$$ $$\arctan x\sim x$$ $$1-\cos(x)\sim\frac{x^2}{2} $$ $$\ln(1+x)\sim x$$ $$e^x-1\sim x$$ $$a^x-1\sim x\ln a$$ $$\sqrt[n]{1+x}-1\sim\frac{x}{n}$$ $$\sqrt[]{1+x}-1\sim\frac{x}{2}$$ $$(1+x)^\alpha\sim1+\alpha x $$ $$1-\sqrt[n]{\cos(mx)}\sim\frac{1}{2n}m^2x^2 $$
3. 基本初等函数的求导公式
$$(1){c}'=0$$ $$(2)(x^u)'= ux^{u-1}$$ $$(3)(\sin x)'= \cos x$$ $$(4)(\cos x)'= -\sin x$$ $$(5)(\tan x)'= \sec^2x$$ $$(6)(\cot x)'= -\csc^2x$$ $$(7)(\sec x)'= \sec x\tan x$$ $$(8)(\csc x)'= -\csc x\cot x$$ $$(9)(e^x)'=e^x$$ $$(10)(a^x)'=a^x\ln a$$ $$(11)(\ln x)'= \frac{1}{x} $$ $$(12)(\log_{a}{x})'= \frac{1}{x \ln a} $$ $$(13)(\arcsin x)'= \frac{1}{\sqrt{1-x^2}} $$ $$(14)(\arccos x)'= -\frac{1}{\sqrt{1-x^2}} $$ $$(15)(\arctan x)'= \frac{1}{1+x^2} $$ $$(16)(\operatorname{arccot} x)'= -\frac{1}{1+x^2} $$ $$(16)[\ln(x+\sqrt{x^2\pm a^2})]'= \frac{1}{\sqrt{x^2\pm a^2}} $$
4.连续与可导
1.$f(x)$连续
$$ \lim_{x \to 0} f(x)=f(0) $$
2.$f(x)$可导=$f'(x)$存在
可导必定连续,连续不一定可导,不连续一定不可导 $$ f'(0)=\lim_{x \to 0}\frac{f(x)-f(0)}{x-0} ,\exists $$
3.$f'(x)$连续
先求导数,分段区间用求导法则,分段点用导数定义
$$ f'(x)=[f(x)]',x\ne 0 $$
$$ f'(0)=\lim_{x \to 0}\frac{f(x)-f(0)}{x-0},x=0 $$
若存在$x>0,x=0,x<0$三个区间
则需要对$x \to 0+,x \to 0-$分别求导
再判断$\lim_{x \to 0}f(x)=f'(0)$
则导函数连续(一阶连续可导)
4.$f'(x)$存在
分段区间对自变量再求导,分段点用导数定义 $$f''(x)=[f'(x)]',x\ne0$$ $$f''(0)=\lim_{x \to 0}\frac{f'(x)-f'(0)}{x-0}\exists$$
5.$f''(x)$连续
1.先求f''(x) (第4步)
2.检验二阶导数值是否等于极限值 $$\lim_{x \to 0}f''(x)=f''(0)$$
5.三角函数基本关系

(1) 对角线上乘积为1
$$ \csc x=\frac{1}{\sin x} $$ $$ \sec x=\frac{1}{\cos x} $$ $$ \cot x=\frac{1}{\tan x} $$
(2) 顶点等于相邻两个顶点乘积
$$ \tan x=\frac{\sin x}{\cos x} $$ $$ \cot x=\frac{\cos x}{\sin x} $$
(3) 阴影三角形上两顶点的平方和等于下顶点的平方
$$ \sin^2x+\cos^2x=1 $$ $$ 1+\tan^2x=\sec^2x $$ $$ 1+\cot^2x=\csc^2x $$
(4) 二倍角公式
$$ \sin 2x=2\sin x\cos x $$ $$ \cos 2x=\cos^2x-\sin^2x= 2\cos^2x-1=1-2\sin^2x$$ $$ \tan 2x=\frac{2\tan x}{1-\tan^2x} $$ $$ \cot 2x=\frac{\cot^2x-1}{2\cot x} $$
(5) 降幂公式(半角公式)
$$ \sin^2x=\frac{1}{2}(1-\cos 2x) $$ $$ \cos^2x=\frac{1}{2}(1+\cos 2x) $$
(6) 和差化积
$$ \sin{\alpha}\cos{\beta}=\frac{1}{2}[\sin(\alpha +\beta)+\sin(\alpha-\beta)] $$ $$ \cos{\alpha}\sin{\beta}=\frac{1}{2}[\sin(\alpha +\beta)-\sin(\alpha-\beta)] $$ $$ \cos{\alpha}\cos{\beta}=\frac{1}{2}[\cos(\alpha +\beta)+\cos(\alpha-\beta)] $$ $$ \sin{\alpha}\sin{\beta}=-\frac{1}{2}[\cos(\alpha +\beta)-\cos(\alpha-\beta)] $$
7.万能公式
令 $ t=\tan{\frac{x}{2}}(-\pi<x<\pi)$
则 $ \sin{x}=\frac{2t}{1+t^2} $, $ \cos{x}=\frac{1-t^2}{1+t^2} $
6.积分
(1)
$$ \int x^\alpha\mathrm{d}x=\frac{1}{\alpha+1}x^{\alpha+1}+c $$ $$ \int \frac{\mathrm{d}t}{\sqrt{t}}=2\sqrt{t}+c $$ $$ \int \frac{\mathrm{d}t}{t^2}=-\frac{1}{t}+c $$ $$ \int e^x\mathrm{d}x=e^x+c $$ $$ \int a^x\mathrm{d}x=\frac{a^x}{\ln a}+c $$ $$ \int \frac{\mathrm{d}x}{x}=ln|x|+c $$ $$ \int\frac{\mathrm{d}x}{\sqrt{1-x^2}} =\arcsin{x}+c $$ $$ \int\frac{\mathrm{d}x}{1+x^2} =\arctan{x}+c $$
(2)
$$\int\frac{\mathrm{d}x}{\sqrt{a^2-x^2}}=\arcsin\frac{x}{a}+c$$ $$\int\frac{\mathrm{d}x}{\sqrt{a^2+x^2}}=\arctan\frac{x}{a}+c = \int\frac{\mathrm{d}x}{\sqrt{x^2+a^2}}=\ln(x+\sqrt{x^2+a^2})+c$$ $$\int\frac{\mathrm{d}x}{a^2+x^2}=\frac{1}{a}\arctan\frac{x}{a}+c$$ $$\int\frac{\mathrm{d}x}{a^2-x^2}=\frac{1}{2a}\ln\left|\frac{a+x}{a-x}\right|+c$$ $$\int\frac{\mathrm{d}x}{x^2-a^2}=\frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right|+c$$ $$\int\frac{\mathrm{d}x}{\sqrt{x^2\pm a^2}}=\ln(x+\sqrt{x^2\pm a^2})+c$$ $$\int\sqrt{x^2-a^2}\mathrm{d}x=\frac{x}{2}\sqrt{x^2-a^2}-\frac{a^2}{2}\ln\left |x+\sqrt{x^2-a^2}\right|+C$$
$$\int\sqrt{a^2+x^2}\mathrm{d}x=\frac{x}{2}\sqrt{a^2+x^2}+\frac{a^2}{2}\ln(x+\sqrt{a^2+x^2})+C$$ $$\int\sqrt{a^2-x^2}\mathrm{d}x=\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}\arcsin\frac{x}{a} +C$$ $$ \int e^{ax}\sin{bx}\mathrm{d}x =\frac{ae^{ax}\sin{bx}-b\cos{bx}e^{ax}}{a^2+b^2}+C $$ $$\int\frac{\mathrm{d}x}{1+e^x}=x-\ln(1+e^x)+c$$
3.含三角函数的
$$ \int \sin x\mathrm{d}x=-\cos x+c $$ $$ \int \cos x\mathrm{d}x=\sin x+c $$ $$ \int\tan{x}\mathrm{d}x=\int\frac{\sin{x}}{\cos{x}}\mathrm{d}x=-\int\frac{\mathrm{d}\cos{x}}{\cos{x}}=-\ln|\cos{x}|+c $$ $$ \int\cot{x}\mathrm{d}x=\int\frac{\cos{x}}{\sin{x}}\mathrm{d}x=\int\frac{\mathrm{d}\sin{x}}{\sin{x}}=\ln|\sin{x}|+c $$
$$ \int\tan^2{x}\mathrm{d}x= \int(\sec^2{x}-1)\mathrm{d}x=\tan{x}-x+C$$ $$ \int\cot^2{x}\mathrm{d}x= \int(\csc^2{x}-1)\mathrm{d}x=-\cot{x}-x+C$$
含有$\sec{x}$的积分
$$\int\sec x\mathrm{d}x=\ln|\sec x+\tan x|+c$$ $$ \int\sec^2{x}\mathrm{d}x=\tan{x}+c $$ $$\int\sec^3x\mathrm{d}x=\frac{1}{2}\sec x\tan x+\frac{1}{2}\ln|\sec x+\tan x|+c$$
含有$\csc{x}$的积分
$$\int\csc x\mathrm{d}x=\ln|\csc x-\cot x|+c$$ $$ \int\csc^2{x}\mathrm{d}x=-\cot{x}+c $$ $$\int\csc^3x\mathrm{d}x=-\frac{1}{2}\csc x\cot x+\frac{1}{2}\ln|\csc x- \cot x|+c$$
$\sin{x}+\cos{x}$
$$ \sin{x}+\cos{x} =\sqrt{2}\sin(x+\frac{\pi}{{4}}) $$
点火公式

区间再现
去掉x
$$\int_{0}^{\pi} xf(\sin{x})\mathrm{d}x=\frac{\pi}{2}\int_{0}^{\pi} f(\sin{x})\mathrm{d}x=\pi\int_{0}^{\frac{\pi}{2}} f(\sin{x})\mathrm{d}x$$
7.因式分解
$$ (a+b)^2=a^2+2ab+b^2 $$ $$ (a-b)^2=a^2-2ab+b^2 $$ $$ (a+b)^3=a^3+3a^2b+3ab^2+b^3 $$ $$ (a-b)^3=a^3-3a^2b+3ab^2-b^3 $$ $$ a^2-b^2=(a+b)(a-b) $$ $$ a^3+b^3=(a+b)(a^2-ab+b^2) $$ $$ a^3-b^3=(a-b)(a^2+ab+b^2) $$
8.闭区间上连续函数的性质
1.最值定理
$$\forall x\in [a,b],m\le f(x)\le M$$
2.有界定理
设$ f(x)$在$[a,b]$上连续,则$f(x)$在$[a,b]$有界
3.零点定理
设$ f(x)$在$[a,b]$上连续,且$f(a)f(b)<0$,则$\exists$ c $\in(a,b)$ 使 $f(c)=0$.
4.介值定理
设$ f(x)$在$[a,b]$上连续,且m和M分别是$f(x)$在$(a,b)$上的最小值和最大值,则$\forall k\in[m,N]$,总$\exists$ c $\in[a,b]$ 使 $f(c)=k$.
9.一元函数微分学
拐点:二阶导数为0和不存在的点 二阶导数>0图像凹,<0图像凸
罗尔定理
$$ 若[a,b]连续,(a,b)可导,且f(a)=f(b),则\exists\varepsilon \in (a,b),使得f'(\varepsilon)=0 $$ 构造辅助函数 $$ f'(\varepsilon)=a\Rightarrow F(x)=f(x)-ax $$ $$ f'(\varepsilon)+kf(\varepsilon)=0\Rightarrow F(x)=e^{kx}f(x)$$ $$ f'(\varepsilon)+g(\varepsilon)f(\varepsilon)=0\Rightarrow F(x)=e^{\int g(x)dx}f(x)$$ $$ \varepsilon f'(\varepsilon)+\lambda f(\varepsilon)=0\Rightarrow F(x)=x^{\lambda}f(x)$$
拉格朗日中值定理
$$ 若[a,b]连续,(a,b)可导,则\exists\xi\in (a,b),使f(b)-f(a)=f'(\xi)(b-a) $$
10. 高阶导数的求法
1.归纳法
求1-3阶导然后观察
2.分解法
通过恒等变形将函数分解、化简后,利用以下基本公式计算 $$ (\frac{1}{a+bx})^{(n)} = (-1)^n\frac{b^n\cdot n!}{(a+bx)^{n+1}}$$ $$ (\sin x)^{(n)} = \sin(x+\frac{n\pi}{2})$$ $$ (\cos x)^{(n)} = \cos(x+\frac{n\pi}{2})$$ $$ [\ln(ax+b)]^{(n)} = \frac{(-1)^{n-1}(n-1)!\cdot a^n}{(ax+b)^n} $$
定积分应用
几何方面
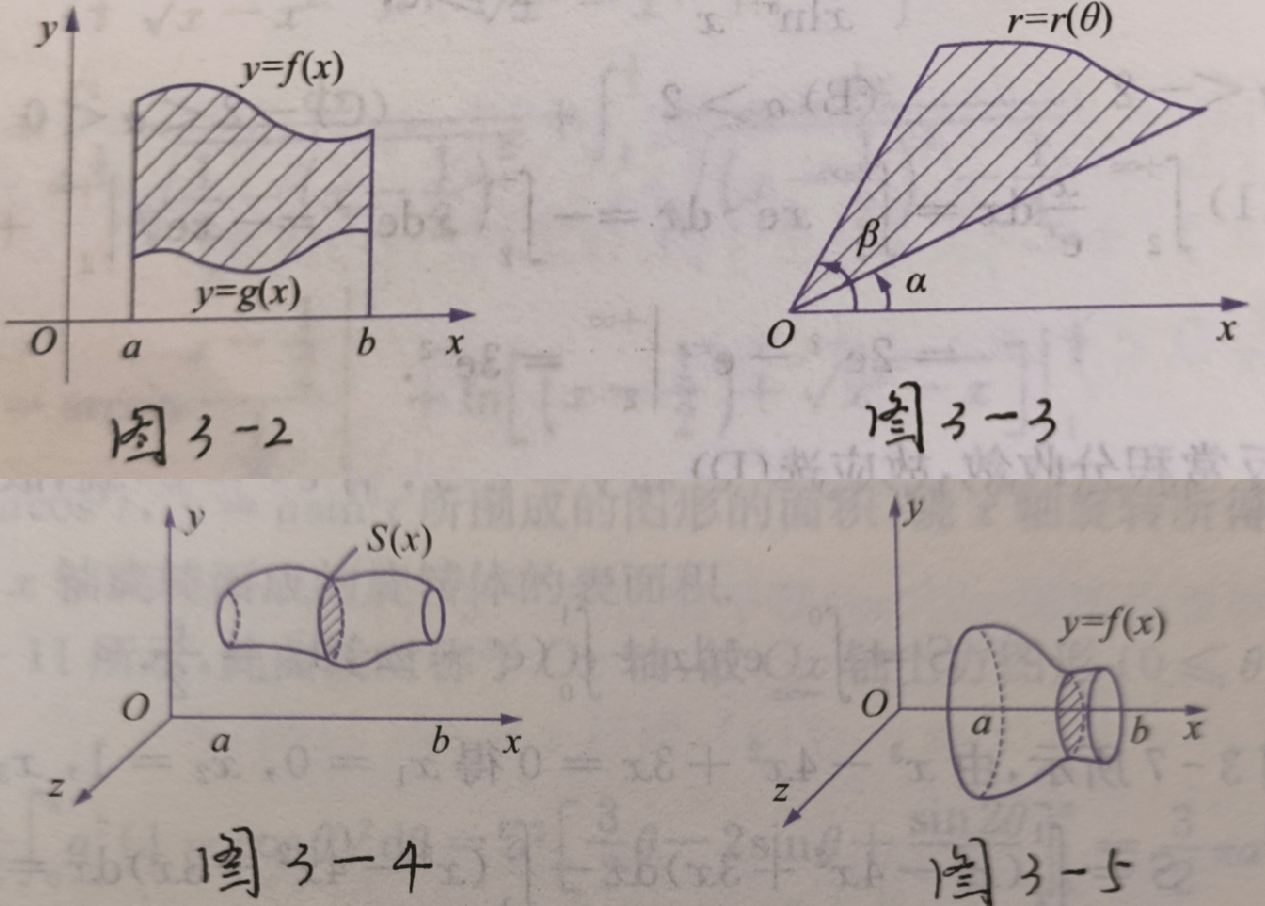
平面图形面积
直角坐标系(图3-2) $$ S=\int_{a}^{b}[f(x)-g(x)]\mathrm{d}x $$ 极坐标系(图3-3) $$ S=\frac{1}{2}\int_{a}^{b}r^2(\theta)\mathrm{d}\theta $$ 参数方程 待补充
几何体体积
图3-4 $$ V_{x} =\int_{a}^{b}s(x)\mathrm{d}x $$ $$ V_{y} =2\pi\int_{a}^{b}xf(x)\mathrm{d}x $$ 图3-5 $$ V=\pi\int_{a}^{b}f^2(x)\mathrm{d}x $$
曲线弧长
直角坐标系 $$ l=\int_{a}^{b}\sqrt{1+f^{'2}(x)}\mathrm{d}x $$ 极坐标系 $$ l=\int_{a}^{b}\sqrt{x^{'2}(t)+y^{'2}(t)}\mathrm{d}t $$ 参数方程
旋转曲面面积
$$ S=2\pi\int_{a}^{b}f(x)\sqrt{1+f^{'2}(x)}\mathrm{d}x $$ 待补充
物理方面
功
待补充
重心
待补充
区间上的平均值公式
$$ \bar{y}=\frac{1}{b-a}\int_{a}^{b}f(x)\mathrm{d}x $$
微分方程
积分因子法
对于 $ y’+p(x)y=q(x) $ 有: $$ y=e^{\int -p(x)\mathrm{d}x}(\int q(x) e^{\int{p(x)\mathrm{d}x} }\mathrm{d}x+C) $$
曲线y的曲率和曲率半径
曲率 $ \frac{|y’’|}{(1+y’^2)^{\frac{3}{2}}} $, 曲率半径=曲率的倒数
伽马公式
$$ \int_{0}^{+\infty}x^ne^{-x}\mathrm{d}x = n! (n正整数) $$
定积分定义求数列极限
$$ \lim_{n \to \infty} \frac{a}{n} \sum_{i=0}^{n} f(\frac{ia}{n})=\int_{0}^{a}f(x)\mathrm{d}x $$
最后修改于 Sun, 02 Apr 2023